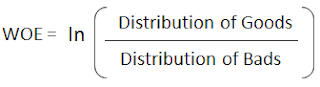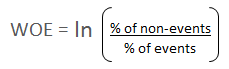The Pearson / Wald / Score Chi-Square Test can be used to test the association between the independent variables and the dependent variable.
A Wald/Score chi-square test can be used for continuous and categorical variables. Whereas, Pearson chi-square is used for categorical variables. The p-value indicates whether a coefficient is significantly different from zero. In logistic regression, we can select top variables based on their high wald chi-square value.
Gain :Gain at a given decile level is the ratio of cumulative number of targets (events) up to that decile to the total number of targets (events) in the entire data set. This is also called CAP (Cumulative Accuracy Profile) in Finance, Credit Risk Scoring Technique
Interpretation: % of targets (events) covered at a given decile level. For example, 80% of targets covered in top 20% of data based on model. In the case of propensity to buy model, we can say we can identify and target 80% of customers who are likely to buy the product by just sending email to 20% of total customers.
Lift : It measures how much better one can expect to do with the predictive model comparing without a model. It is the ratio of gain % to the random expectation % at a given decile level. The random expectation at the xth decile is x%.
Interpretation: The Cum Lift of 4.03 for top two deciles, means that when selecting 20% of the records based on the model, one can expect 4.03 times the total number of targets (events) found by randomly selecting 20%-of-file without a model.
Gain / Lift Analysis
- Randomly split data into two samples: 70% = training sample, 30% = validation sample.
- Score (predicted probability) the validation sample using the response model under consideration.
- Rank the scored file, in descending order by estimated probability
- Split the ranked file into 10 sections (deciles)
- Number of observations in each decile
- Number of actual events in each decile
- Number of cumulative actual events in each decile
- Percentage of cumulative actual events in each decile. It is called Gain Score.
- Divide the gain score by % of data used in each portion of 10 bins. For example, in second decile, divide gain score by 20.
| Decile
Rank |
Number of cases |
Number of
Responses |
Cumulative
Responses |
% of Events |
Gain |
Cumulative Lift |
Number of
Decile Score to divide Gain |
| 1 |
2500 |
2179 |
2179 |
44.71% |
44.71% |
4.47% |
10 |
| 2 |
2500 |
1753 |
3932 |
35.97% |
80.67% |
4.03% |
20 |
| 3 |
2500 |
396 |
4328 |
8.12% |
88.80% |
2.96% |
30 |
| 4 |
2500 |
111 |
4439 |
2.28% |
91.08% |
2.28% |
40 |
| 5 |
2500 |
110 |
4549 |
2.26% |
93.33% |
1.87% |
50 |
| 6 |
2500 |
85 |
4634 |
1.74% |
95.08% |
1.58% |
60 |
| 7 |
2500 |
67 |
4701 |
1.37% |
96.45% |
1.38% |
70 |
| 8 |
2500 |
69 |
4770 |
1.42% |
97.87% |
1.22% |
80 |
| 9 |
2500 |
49 |
4819 |
1.01% |
98.87% |
1.10% |
90 |
| 10 |
2500 |
55 |
4874 |
1.13% |
100.00% |
1.00% |
100 |
| |
25000 |
4874 |
|
|
|
|
|
Detecting Outliers
There are two simple ways you can detect outlier problem :
1. Box Plot Method : If a value is higher than the 1.5*IQR above the upper quartile (Q3), the value will be considered as outlier. Similarly, if a value is lower than the 1.5*IQR below the lower quartile (Q1), the value will be considered as outlier.
QR is interquartile range. It measures dispersion or variation. IQR = Q3 -Q1.
Lower limit of acceptable range = Q1 - 1.5* (Q3-Q1)
Upper limit of acceptable range = Q3 + 1.5* (Q3-Q1)
Some researchers use 3 times of interquartile range instead of 1.5 as cutoff. If a high percentage of values are appearing as outliers when you use 1.5*IQR as cutoff, then you can use the following rule
Lower limit of acceptable range = Q1 - 3* (Q3-Q1)
Upper limit of acceptable range = Q3 + 3* (Q3-Q1)
2. Standard Deviation Method: If a value is higher than the mean plus or minus three Standard Deviation is considered as outlier. It is based on the characteristics of a normal distribution for which 99.87% of the data appear within this range.
Acceptable Range : The mean plus or minus three Standard Deviation
This method has several shortcomings :
- The mean and standard deviation are strongly affected by outliers.
- It assumes that the distribution is normal (outliers included)
- It does not detect outliers in small samples
3. Percentile Capping (Winsorization): In layman's terms,
Winsorization (Winsorizing) at 1st and 99th percentile implies values that are less than the value at 1st percentile are replaced by the value at 1st percentile, and values that are greater than the value at 99th percentile are replaced by the value at 99th percentile. The winsorization at 5th and 95th percentile is also common.
The box-plot method is less affected by extreme values as compared to Standard Deviation method. If the distribution is skewed, the box-plot method fails. The Winsorization method is a industry standard technique to treat outliers. It works well. In contrast, box-plot and standard deviation methods are traditional methods to treat outliers.
4. Weight of Evidence: Logistic regression model is one of the most commonly used statistical technique for solving binary classification problem. It is an acceptable technique in almost all the domains. These two concepts - weight of evidence (WOE) and information value (IV) evolved from the same logistic regression technique. These two terms have been in existence in credit scoring world for more than 4-5 decades. They have been used as a benchmark to screen variables in the credit risk modeling projects such as probability of default. They help to explore data and screen variables. It is also used in marketing analytics project such as customer attrition model, campaign response model etc.
What is Weight of Evidence (WOE)?
The weight of evidence tells the predictive power of an independent variable in relation to the dependent variable. Since it evolved from credit scoring world, it is generally described as a measure of the separation of good and bad customers. "Bad Customers" refers to the customers who defaulted on a loan. and "Good Customers" refers to the customers who paid back loan.
Formulae - ln(% of Good Customers / % of Bad Customer)
Distribution of Goods - % of Good Customers in a particular group
Distribution of Bads - % of Bad Customers in a particular group
ln - Natural Log
Positive WOE means Distribution of Goods > Distribution of Bads
Negative WOE means Distribution of Goods < Distribution of Bads
Hint : Log of a number > 1 means positive value. If less than 1, it means negative value.
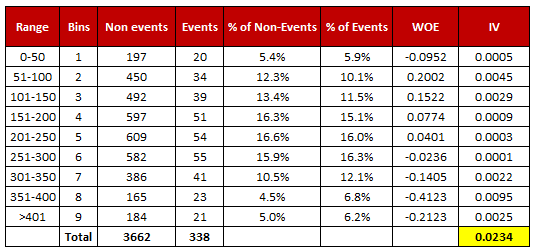
Many people do not understand the terms goods/bads as they are from different background than the credit risk. It's good to understand the concept of WOE in terms of events and non-events. It is calculated by taking the natural logarithm (log to base e) of division of % of non-events and % of events.
Weight of Evidence for a category = log (% events / % non-events) in the category
Weight of Evidence was originated from logistic regression technique. It tells the predictive power of an independent variable in relation to the dependent variable. It is calculated by taking the natural logarithm (log to base e) of division of % of non-events and % of events.
Outlier Treatment with Weight Of Evidence : Outlier classes are grouped with other categories based on Weight of Evidence (WOE).
- For a continuous variable, split data into 10 parts (or lesser depending on the distribution).
- Calculate the number of events and non-events in each group (bin)
- Calculate the % of events and % of non-events in each group.
- Calculate WOE by taking natural log of division of % of non-events and % of events
Note : For a categorical variable, you do not need to split the data (Ignore Step 1 and follow the remaining steps)
WEIGHT OF EVIDENCE (WOE) AND INFORMATION VALUE (IV) EXPLAINED
In this article, we will cover the concept of weight of evidence and information value and how they are used in predictive modeling process along with details of how to compute them using SAS, R and Python.
Logistic regression model is one of the most commonly used statistical technique for solving binary classification problem. It is an acceptable technique in almost all the domains. These two concepts - weight of evidence (WOE) and information value (IV) evolved from the same logistic regression technique. These two terms have been in existence in credit scoring world for more than 4-5 decades. They have been used as a benchmark to screen variables in the credit risk modeling projects such as probability of default. They help to explore data and screen variables. It is also used in marketing analytics project such as customer attrition model, campaign response model etc.
What is Weight of Evidence (WOE)?
The weight of evidence tells the predictive power of an independent variable in relation to the dependent variable. Since it evolved from credit scoring world, it is generally described as a measure of the separation of good and bad customers.
"Bad Customers" refers to the customers who defaulted on a loan. and
"Good Customers" refers to the customers who paid back loan.
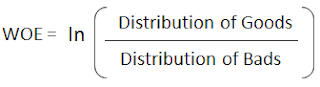 |
| WOE Calculation |
Distribution of Goods - % of Good Customers in a particular group
Distribution of Bads - % of Bad Customers in a particular group
ln - Natural Log
Positive WOE means Distribution of Goods > Distribution of Bads
Negative WOE means Distribution of Goods < Distribution of Bads
Hint : Log of a number > 1 means positive value. If less than 1, it means negative value.
Many people do not understand the terms goods/bads as they are from different background than the credit risk. It's good to understand the concept of WOE in terms of
events and non-events. It is calculated by taking the natural logarithm (log to base e) of division of % of non-events and % of events.
WOE = In(% of non-events ➗ % of events)
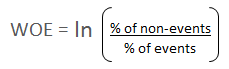 |
| Weight of Evidence Formula |
Steps of Calculating WOE
- For a continuous variable, split data into 10 parts (or lesser depending on the distribution).
- Calculate the number of events and non-events in each group (bin)
- Calculate the % of events and % of non-events in each group.
- Calculate WOE by taking natural log of division of % of non-events and % of events
Note : For a categorical variable, you do not need to split the data (Ignore Step 1 and follow the remaining steps)
 |
| Weight of Evidence and Information Value Calculation |
Terminologies related to WOE
1. Fine Classing : Create 10/20 bins/groups for a continuous independent variable and then calculates WOE and IV of the variable
2. Coarse Classing : Combine adjacent categories with similar WOE scores
Weight of Evidence (WOE) helps to transform a continuous independent variable into a set of groups or bins based on similarity of dependent variable distribution i.e. number of events and non-events.
For continuous independent variables : First, create bins (categories / groups) for a continuous independent variable and then combine categories with similar WOE values and replace categories with WOE values. Use WOE values rather than input values in your model.
WEIGHT OF EVIDENCE (WOE) AND INFORMATION VALUE (IV) EXPLAINED
In this article, we will cover the concept of weight of evidence and information value and how they are used in predictive modeling process along with details of how to compute them using SAS, R and Python.
Logistic regression model is one of the most commonly used statistical technique for solving binary classification problem. It is an acceptable technique in almost all the domains. These two concepts - weight of evidence (WOE) and information value (IV) evolved from the same logistic regression technique. These two terms have been in existence in credit scoring world for more than 4-5 decades. They have been used as a benchmark to screen variables in the credit risk modeling projects such as probability of default. They help to explore data and screen variables. It is also used in marketing analytics project such as customer attrition model, campaign response model etc.
What is Weight of Evidence (WOE)?
The weight of evidence tells the predictive power of an independent variable in relation to the dependent variable. Since it evolved from credit scoring world, it is generally described as a measure of the separation of good and bad customers.
"Bad Customers" refers to the customers who defaulted on a loan. and
"Good Customers" refers to the customers who paid back loan.
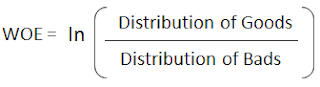 |
| WOE Calculation |
Distribution of Goods - % of Good Customers in a particular group
Distribution of Bads - % of Bad Customers in a particular group
ln - Natural Log
Positive WOE means Distribution of Goods > Distribution of Bads
Negative WOE means Distribution of Goods < Distribution of Bads
Hint : Log of a number > 1 means positive value. If less than 1, it means negative value.
Many people do not understand the terms goods/bads as they are from different background than the credit risk. It's good to understand the concept of WOE in terms of
events and non-events. It is calculated by taking the natural logarithm (log to base e) of division of % of non-events and % of events.
WOE = In(% of non-events ➗ % of events)
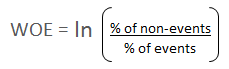 |
| Weight of Evidence Formula |
Steps of Calculating WOE
- For a continuous variable, split data into 10 parts (or lesser depending on the distribution).
- Calculate the number of events and non-events in each group (bin)
- Calculate the % of events and % of non-events in each group.
- Calculate WOE by taking natural log of division of % of non-events and % of events
Note : For a categorical variable, you do not need to split the data (Ignore Step 1 and follow the remaining steps)
 |
| Weight of Evidence and Information Value Calculation |
Download :
Excel Template for WOE and IVTerminologies related to WOE
1. Fine ClassingCreate 10/20 bins/groups for a continuous independent variable and then calculates WOE and IV of the variable
2. Coarse ClassingCombine adjacent categories with similar WOE scores
Usage of WOE
Weight of Evidence (WOE) helps to transform a continuous independent variable into a set of groups or bins based on similarity of dependent variable distribution i.e. number of events and non-events.
For continuous independent variables : First, create bins (categories / groups) for a continuous independent variable and then combine categories with similar WOE values and replace categories with WOE values. Use WOE values rather than input values in your model.
Categorical independent variables: Combine categories with similar WOE and then create new categories of an independent variable with continuous WOE values. In other words, use WOE values rather than raw categories in your model. The transformed variable will be a continuous variable with WOE values. It is same as any continuous variable.
Why combine categories with similar WOE?
It is because the categories with similar WOE have almost same proportion of events and non-events. In other words, the behavior of both the categories is same.
Rules related to WOE
- Each category (bin) should have at least 5% of the observations.
- Each category (bin) should be non-zero for both non-events and events.
- The WOE should be distinct for each category. Similar groups should be aggregated.
- The WOE should be monotonic, i.e. either growing or decreasing with the groupings.
- Missing values are binned separately.
FEATURE SELECTION : SELECT IMPORTANT VARIABLES WITH BORUTA PACKAGE
FEATURE SELECTION : SELECT IMPORTANT VARIABLES WITH BORUTA PACKAGE
This article explains how to select important variables using boruta package in R. Variable Selection is an important step in a predictive modeling project. It is also called 'Feature Selection'. Every private and public agency has started tracking data and collecting information of various attributes. It results to access to too many predictors for a predictive model. But not every variable is important for prediction of a particular task. Hence it is essential to identify important variables and remove redundant variables. Before building a predictive model, it is generally not know the exact list of important variable which returns accurate and robust model.
Why Variable Selection is important?
- Removing a redundant variable helps to improve accuracy. Similarly, inclusion of a relevant variable has a positive effect on model accuracy.
- Too many variables might result to overfitting which means model is not able to generalize pattern
- Too many variables leads to slow computation which in turns requires more memory and hardware.
Why Boruta Package?There are a lot of packages for feature selection in R. The question arises " What makes boruta package so special". See the following reasons to use boruta package for feature selection.
- It works well for both classification and regression problem.
- It takes into account multi-variable relationships.
- It is an improvement on random forest variable importance measure which is a very popular method for variable selection.
- It follows an all-relevant variable selection method in which it considers all features which are relevant to the outcome variable. Whereas, most of the other variable selection algorithms follow a minimal optimal method where they rely on a small subset of features which yields a minimal error on a chosen classifier.
- It can handle interactions between variables
- It can deal with fluctuating nature of random a random forest importance measure
Basic Idea of Boruta Algorithm
Perform shuffling of predictors' values and join them with the original predictors and then build random forest on the merged dataset. Then make comparison of original variables with the randomised variables to measure variable importance. Only variables having higher importance than that of the randomised variables are considered important.
How Boruta Algorithm Works
Follow the steps below to understand the algorithm -
- Create duplicate copies of all independent variables. When the number of independent variables in the original data is less than 5, create at least 5 copies using existing variables.
- Shuffle the values of added duplicate copies to remove their correlations with the target variable. It is called shadow features or permuted copies.
- Combine the original ones with shuffled copies
- Run a random forest classifier on the combined dataset and performs a variable importance measure (the default is Mean Decrease Accuracy) to evaluate the importance of each variable where higher means more important.
- Then Z score is computed. It means mean of accuracy loss divided by standard deviation of accuracy loss.
- Find the maximum Z score among shadow attributes (MZSA)
- Tag the variables as 'unimportant' when they have importance significantly lower than MZSA. Then we permanently remove them from the process.
- Tag the variables as 'important' when they have importance significantly higher than MZSA.
- Repeat the above steps for predefined number of iterations (random forest runs), or until all attributes are either tagged 'unimportant' or 'important', whichever comes first.
Major Disadvantages: Boruta does not treat collinearity while selecting important variables. It is because of the way algorithm works.
In Linear Regression:
There are two important metrics that helps evaluate the model - Adjusted R-Square and Mallows' Cp Statistics.
Adjusted R-Square: It penalizes the model for inclusion of each additional variable. Adjusted R-square would increase only if the variable included in the model is significant. The model with the larger adjusted R-square value is considered to be the better model.
Mallows' Cp Statistic: It helps detect model biasness, which refers to either underfitting the model or overfitting the model.
Formulae : Mallows Cp = (SSE/MSE) – (n – 2p)
where SSE is Sum of Squared Error and MSE is Mean Squared Error with all independent variables in model and p is for the number of estimates in model (i.e. number of independent variables plus intercept).
Rules to select best model: Look for models where
Cp is less than or equal to p, which is the number of independent variables plus intercept.A final model should be selected based on the following two criteria's -
First Step : Models in which number of variables where Cp is less than or equal to p
Second Step : Select model in which fewest parameters exist. Suppose two models have Cp less than or equal to p. First Model - 5 Variables, Second Model - 6 Variables. We should select first model as it contains fewer parameters.
Important Note :
To select the best model for
parameter estimation, you should use Hocking's criterion for Cp.
For parameter estimation, Hocking recommends a model where Cp<=2p – pfull +1, where p is the number of parameters in the model, including the intercept. pfull - total number of parameters (initial variable list) in the model.
To select the best model for prediction, you should use Mallows' criterion for Cp.
How to check non-linearity
In linear regression analysis, it's an important assumption that there should be a linear relationship between independent variable and dependent variable. Whereas, logistic regression assumes there should be a linear relationship between independent variable and logit function.
-
Pearson correlation is a measure of linear relationship. The variables must be measured at interval scales. It is sensitive to outliers. If pearson correlation coefficient of a variable is close to 0, it means there is no linear relationship between variables.
-
Spearman's correlation is a measure of monotonic relationship. It can be used for ordinal variables. It is less sensitive to outliers. If spearman correlation coefficient of a variable is close to 0, it means there is no monotonic relationship between variables.
-
Hoeffding’s D correlation is a measure of linear, monotonic and non-monotonic relationship. It has values between –0.5 to 1. The signs of Hoeffding coefficient has no interpretation.
If a variable has a very low rank for Spearman (coefficient - close to 0) and a very high rank for Hoeffding indicates a non-monotonic relationship.
If a variable has a very low rank for Pearson (coefficient - close to 0) and a very high rank for Hoeffding indicates a non-linear relationship.
Appendix: